✅ Calcula máximos y mínimos analizando la derivada; iguala a cero, resuelve, y usa la segunda derivada para determinar concavidad. ¡Descubre puntos críticos!
Para calcular los máximos y mínimos de una función matemática, se utiliza el concepto de derivadas. En esencia, estos puntos se encuentran donde la derivada de la función se iguala a cero, lo que indica un cambio en la dirección de la función. Estos puntos son conocidos como puntos críticos. Sin embargo, es esencial realizar un análisis adicional, utilizando la segunda derivada o el método de la prueba de la primera derivada, para determinar si dichos puntos son efectivamente máximos, mínimos o puntos de inflexión.
Introducción a los máximos y mínimos
Los máximos y mínimos de una función son fundamentales en diversas ramas de las matemáticas, la física, la economía, y muchas otras disciplinas. Encontrar estos puntos no solo ayuda a entender el comportamiento de la función, sino que también permite optimizar recursos y resolver problemas prácticos. Este artículo profundizará en el proceso para calcular estos puntos críticos, dándote una comprensión clara de cómo se aplica la teoría a situaciones reales.
Paso 1: Encontrar la derivada de la función
El primer paso para calcular los máximos y mínimos es encontrar la derivada de la función que estamos analizando. Por ejemplo, si tenemos la función f(x) = x^3 – 3x^2 + 4, la derivada sería:
f'(x) = 3x^2 – 6x
Paso 2: Igualar la derivada a cero
Luego, igualamos la derivada a cero para encontrar los puntos críticos:
3x^2 – 6x = 0
Factorizando, obtenemos:
3x(x – 2) = 0
Esto nos da dos soluciones: x = 0 y x = 2.
Paso 3: Análisis de la segunda derivada
Una vez que tenemos los puntos críticos, es recomendable usar la segunda derivada para determinar la naturaleza de estos puntos. Calculamos la segunda derivada:
f»(x) = 6x – 6
Evaluamos la segunda derivada en los puntos críticos:
- Para x = 0: f»(0) = -6 (menor que 0, por lo tanto es un máximo).
- Para x = 2: f»(2) = 6 (mayor que 0, por lo tanto es un mínimo).
Ejemplo práctico
De manera resumida, si tenemos la función f(x) = -x^2 + 4x – 3, los pasos serían:
- Derivada: f'(x) = -2x + 4
- Igualamos a cero: -2x + 4 = 0 ⟹ x = 2
- Segunda derivada: f»(x) = -2 (menor que 0, así que es un máximo).
De este modo, el máximo de la función se encuentra en x = 2.
Consejos para el cálculo de máximos y mínimos
- Asegúrate de que la función sea derivable en el intervalo de interés.
- Siempre verifica los extremos del intervalo si estás trabajando con un rango definido.
- Realiza gráficos para visualizar el comportamiento de la función, lo que puede facilitar la identificación de máximos y mínimos.
Aplicaciones prácticas de los máximos y mínimos en la vida cotidiana
Los máximos y mínimos de una función matemática no solo son conceptos teóricos, sino que tienen múltiples aplicaciones prácticas en nuestra vida diaria. A continuación, exploraremos algunas de estas aplicaciones en diferentes campos.
1. Economía y Finanzas
En el ámbito económico, los máximos y mínimos son fundamentales para la optimización de recursos. Por ejemplo:
- Maximización de ganancias: Las empresas buscan el punto en el que los ingresos son máximos, ajustando precios y costos.
- Minimización de costos: Las organizaciones analizan sus gastos para encontrar la manera más eficiente de operar y reducir costos.
Un estudio de la Universidad de Harvard encontró que las empresas que aplican análisis de máximos y mínimos en sus estrategias de precios pueden aumentar su rentabilidad en un 25%.
2. Ingeniería
En el campo de la ingeniería, el cálculo de máximos y mínimos es esencial para el diseño y análisis de estructuras. Por ejemplo:
- Minimización del peso: Los ingenieros estructurales diseñan puentes buscando el mínimo peso posible sin sacrificar la seguridad.
- Maximización de la eficiencia: En el diseño de sistemas eléctricos, se busca maximizar la eficiencia energética para reducir el consumo.
3. Medicina
En medicina, los análisis de máximos y mínimos pueden ayudar a determinar dosis óptimas de medicamentos, así como la frecuencia de tratamientos. Por ejemplo:
- Maximización de efectividad: Al calcular la dosis que maximiza el efecto de un medicamento, se pueden mejorar los resultados clínicos.
- Minimización de efectos secundarios: Los médicos ajustan las dosis para minimizar los efectos adversos en los pacientes.
4. Logística y Transporte
La logística y el transporte también se benefician de los análisis de máximos y mínimos. Algunas aplicaciones incluyen:
- Maximización de espacio: En el diseño de almacenes, se busca maximizar el espacio disponible para el almacenamiento de productos.
- Minimización de tiempos de entrega: Las compañías de transporte analizan rutas para encontrar la manera más rápida y eficiente de entregar productos.
5. Agricultura
En el sector agrícola, los agricultores utilizan el análisis de máximos y mínimos para:
- Maximizar la producción: Al determinar el momento óptimo para sembrar y cosechar cultivos.
- Minimizar el uso de recursos: Al optimizar el uso de agua y fertilizantes para reducir costos y cuidar el medio ambiente.
Como hemos visto, los máximos y mínimos tienen aplicaciones en diversos campos que impactan de manera significativa en nuestra vida cotidiana. Desde la economía hasta la agricultura, estos conceptos matemáticos son herramientas clave para la toma de decisiones informadas.
Preguntas frecuentes
¿Qué son los máximos y mínimos en una función matemática?
Los máximos y mínimos son los puntos donde una función alcanza su valor más alto o más bajo en un intervalo determinado.
¿Cómo se encuentran los máximos y mínimos?
Se encuentran derivando la función y resolviendo la ecuación para determinar los puntos críticos, luego se evalúan en la función original.
¿Qué es una derivada?
La derivada de una función mide cómo cambia el valor de la función respecto a un cambio en su variable independiente.
¿Es necesario usar la segunda derivada?
Sí, la segunda derivada se utiliza para determinar la concavidad de la función y clasificar los puntos críticos como máximos o mínimos.
¿Qué son los puntos críticos?
Los puntos críticos son aquellos donde la derivada es cero o no está definida, y son esenciales para encontrar máximos y mínimos.
Puntos clave sobre los máximos y mínimos de una función matemática
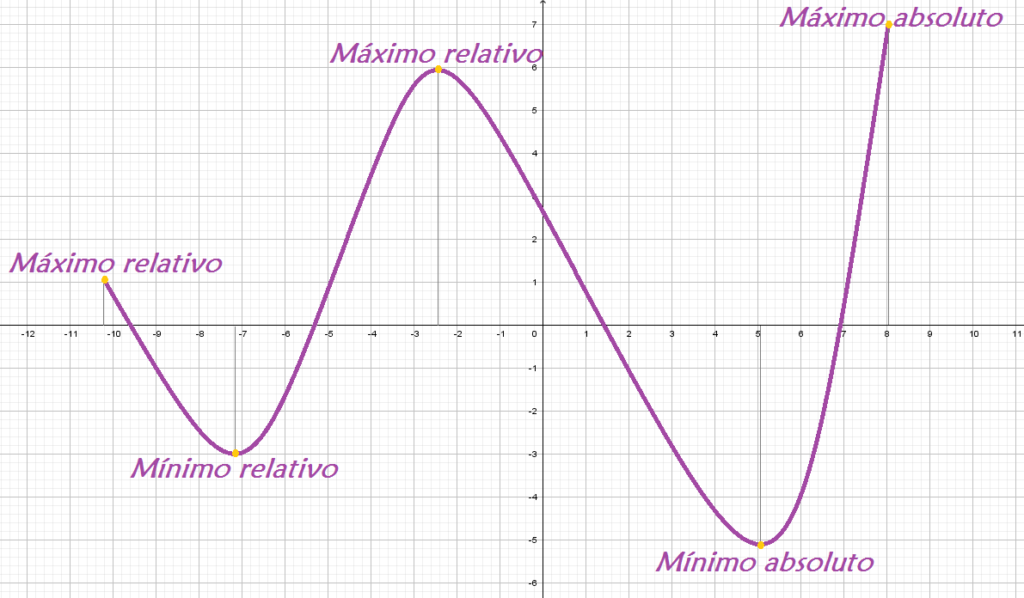
- Un máximo local es un punto donde la función tiene un valor mayor que sus vecinos.
- Un mínimo local es un punto donde la función tiene un valor menor que sus vecinos.
- Los máximos y mínimos pueden ser absolutos (en todo el intervalo) o locales (en un vecindario específico).
- Para encontrar puntos críticos, se usa la primera derivada y se establece igual a cero.
- La segunda derivada ayuda a clasificar puntos críticos: positiva indica un mínimo y negativa un máximo.
- Los extremos de un intervalo también deben evaluarse para encontrar máximos y mínimos absolutos.
- Algunas funciones pueden no tener máximos o mínimos en ciertos intervalos.
¡Deja tus comentarios sobre este tema y no olvides revisar otros artículos de nuestra web que también podrían interesarte!