✅ Charles H. Lehmann enseña conceptos como coordenadas cartesianas, ecuaciones de rectas y cónicas, transformaciones geométricas y análisis vectorial.
Charles H. Lehmann en su obra sobre Geometría Analítica enseña diversos conceptos fundamentales que son cruciales para entender esta rama de las matemáticas. Entre los más destacados se encuentran la representación de puntos en el plano, el análisis de rectas y su ecuación, así como el estudio de las curvas y figuras geométricas en el espacio tridimensional. Además, enfatiza la importancia de la intersección de líneas y planos, lo que resulta esencial para resolver problemas geométricos complejos.
La Geometría Analítica es una herramienta poderosa que combina la geometría con el álgebra, permitiendo resolver problemas visuales mediante el uso de ecuaciones. Lehmann, a través de su enfoque metódico, proporciona a los estudiantes las bases necesarias para abordar estos conceptos de manera clara y efectiva. Exploraremos en detalle los conceptos centrales que presenta Lehmann y cómo estos se aplican en situaciones prácticas.
Conceptos Fundamentales de la Geometría Analítica
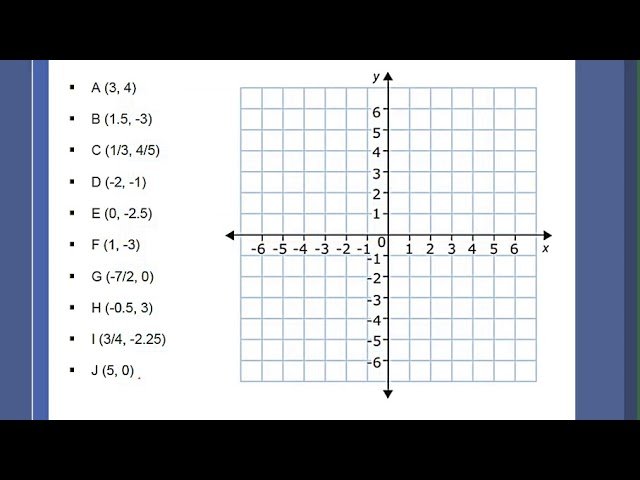
- Puntos en el Plano: Se presentan las coordenadas cartesianas y cómo se representan los puntos en un plano.
- Ecuaciones de Rectas: Se estudian diferentes formas de la ecuación de una recta, incluyendo la forma pendiente-intersección y la forma general.
- Intersecciones: Análisis de cómo encontrar la intersección de dos o más rectas, así como la intersección de rectas con figuras geométricas.
- Curvas y Figuras: Exploración de ecuaciones que representan parábolas, hipérbolas y elipses.
- Distancias y Ángulos: Cálculos para determinar la distancia entre dos puntos y el ángulo entre dos rectas.
Impacto en la Educación Matemática
El enfoque de Lehmann en la Geometría Analítica no solo proporciona herramientas para resolver problemas matemáticos, sino que también desarrolla el pensamiento crítico y la capacidad de resolución de problemas en los estudiantes. Su metodología permite a los alumnos comprender la aplicación práctica de estos conceptos en campos como la física, la ingeniería y la arquitectura.
Ejemplos Prácticos
Por ejemplo, al trabajar con la ecuación de una recta, los estudiantes pueden entender cómo se aplica en la trazabilidad de rutas en un plano o cómo se diseñan estructuras arquitectónicas. Además, los ejercicios propuestos por Lehmann fomentan la participación activa y el análisis crítico de los problemas presentados, lo que mejora la experiencia de aprendizaje.
Aplicaciones prácticas de la geometría analítica en la vida cotidiana
La geometría analítica no solo es un concepto académico, sino que tiene numerosas aplicaciones prácticas que impactan nuestra vida diaria. Aquí exploraremos algunas de las formas más comunes en que utilizamos estos principios en situaciones cotidianas.
1. Navegación y mapas
La geometría analítica juega un papel crucial en la navegación. Los sistemas de GPS utilizan coordenadas cartesianas para determinar la ubicación exacta de un usuario. Esto se traduce en:
- Coordenadas. Las posiciones se representan mediante pares de coordenadas (x, y), lo que permite calcular distancias y rutas.
- Mapas digitales. Aplicaciones como Google Maps utilizan algoritmos basados en geometría analítica para ofrecer rutas óptimas.
2. Arquitectura y diseño urbano
En el ámbito de la arquitectura y el diseño urbano, la geometría analítica es esencial para:
- Crear planos de edificios y espacios públicos.
- Realizar análisis estructural para garantizar la seguridad y estabilidad de las construcciones.
Por ejemplo, el cálculo de áreas y volúmenes de edificios se basa en la geometría analítica, permitiendo a los arquitectos optimizar el uso del espacio.
3. Diseño gráfico y arte
Los diseñadores gráficos utilizan principios de geometría analítica para crear composiciones visuales atractivas. A través de:
- Proporciones. Aplicar la regla de tercios y otros principios de diseño geométrico.
- Transformaciones. Utilizar rotaciones, escalados y traslaciones para ajustar elementos visuales.
4. Física y ciencias naturales
En las ciencias naturales, la geometría analítica se utiliza para describir fenómenos físicos. Por ejemplo:
- Trayectorias de proyectiles. La ecuación de la parábola se aplica para predecir la trayectoria de objetos lanzados.
- Movimiento de partículas. Se utilizan coordenadas para analizar el movimiento en diferentes dimensiones.
5. Economía y finanzas
En el ámbito de la economía, la geometría analítica se utiliza en la representación de datos. Esto incluye:
- Gráficas de oferta y demanda. Permiten visualizar la relación entre precios y cantidades.
- Análisis de tendencias. Ayuda a proyectar comportamientos futuros en el mercado.
Ejemplo práctico
Consideremos un ejemplo sencillo relacionado con la navegación:
- Supongamos que estás en una ciudad y deseas llegar a un restaurante a 3 km al norte y 4 km al este.
- Utilizando el teorema de Pitágoras, puedes calcular la distancia directa: d = √(3^2 + 4^2) = 5 km.
- Este cálculo es esencial para determinar la mejor ruta y tiempo estimado de llegada.
Las aplicaciones de la geometría analítica son variadas y se presentan en múltiples aspectos de nuestra vida diaria, desde la navegación hasta la arquitectura y más allá. Con una comprensión adecuada de estos conceptos, podemos mejorar la eficiencia y efectividad en diversas áreas.
Preguntas frecuentes
¿Quién fue Charles H. Lehmann?
Charles H. Lehmann fue un destacado matemático conocido por sus contribuciones en geometría analítica y educación matemática.
¿Qué es la geometría analítica?
La geometría analítica es una rama de las matemáticas que estudia las relaciones entre geometría y álgebra mediante el uso de coordenadas y ecuaciones.
¿Cuáles son los conceptos clave en su obra?
Lehmann destaca conceptos como puntos, líneas, planos, distancias, y la representación gráfica de ecuaciones algebraicas.
¿Qué aplicaciones tiene la geometría analítica?
Se utiliza en diversas áreas como la física, ingeniería, diseño gráfico y en la resolución de problemas espaciales.
¿Cómo se relaciona la geometría analítica con otras ramas matemáticas?
Se relaciona estrechamente con el álgebra, la trigonometría y el cálculo, facilitando la comprensión de fenómenos en el espacio.
Puntos clave sobre la geometría analítica y Charles H. Lehmann
- Charles H. Lehmann contribuyó significativamente a la enseñanza de la geometría analítica.
- Se centra en la conexión entre la geometría y el álgebra.
- Los conceptos fundamentales incluyen:
- Puntos y coordenadas
- Líneas rectas y pendientes
- Distancias y fórmulas de distancia
- Intersecciones y planos
- Representación gráfica de ecuaciones
- Importancia en la resolución de problemas en diversas disciplinas.
- Base para el desarrollo de conceptos más avanzados en matemáticas.
¡Nos gustaría saber tu opinión! Deja tus comentarios y no olvides revisar otros artículos en nuestro sitio web que también podrían interesarte.